The radion refractive index structure of the atmosphere

The refractive index of the atmosphere, n, at radio frequencies between HF and UHF is given by:

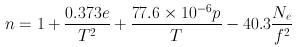
where:

e - partial pressure of water vapour (hPa)

T - absolute temperature (K)

p - atmospheric pressure (hPa)

N_e - number density of free electrons (m^-3)

f - radio frequency (MHz)

Since the magnitudes of the deviations from 1.0 are very small, it is useful to define the refractivity, N, where:

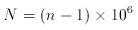
The first term, in the top equation, represents the 'humidity' contribution. Water molecules have a dipole moment which varies with the frequency of the incident electromagnetic radiation. At visible light frequencies only the polarised electric field of the water molecules contributes. For the range HF to UHF, however, the water molecules can additionally reorient themselves rapidly enough to follow the changes of the incident electric field. The second term represents the 'density' contribution. The third term only begins to become signficant at altitudes above 50 km. The figure below shows the relative contributions of the humidity and density terms to the refractivity based on the U.S. Standard Atmosphere 1976 (temperature profile shown in the left panel) for altitudes up to 20 km.

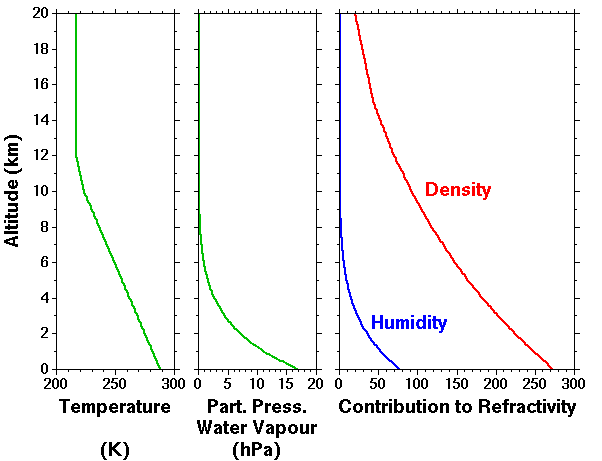
The profile of partial pressure of water vapour is assumed to follow the saturation vapour pressure, e_s, for the given temperature profile, i.e. for 100% relative humidity at all altitudes, where:

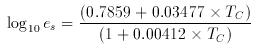
and T_C is the temperature in °C, which is related to the absolute temperature by

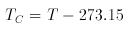
Despite the fact that the (maximum possible) humidity contribution is smaller than the density contribution at all altitudes, the radar return signal power for clear air returns is related to the vertical gradient of the refractive index; the humidity contribution can dominate for altitudes up to the (almost) the tropopause level.

Internal Links:

Return to top of page

Clear-air radar return mechanisms