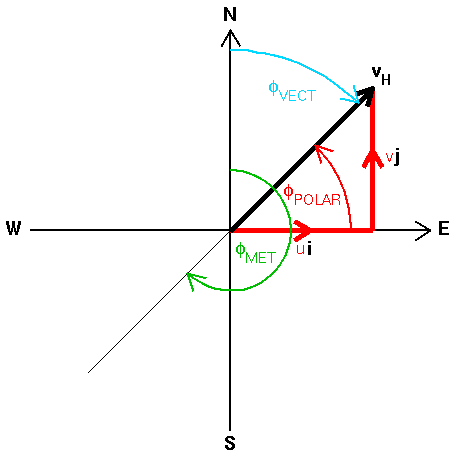
The wind vector can be expressed either in terms of orthogonal veocity components, where:
- u is the ZONAL
VELOCITY, i.e. the component of the horizontal wind TOWARDS EAST.
- v is the MERIDIONAL VELOCITY, i.e. the component of the horizontal wind TOWARDS NORTH.
- (the symbol w is used for the VERTICAL VELOCITY, which is typically +ve for an upward velocity).
- v is the MERIDIONAL VELOCITY, i.e. the component of the horizontal wind TOWARDS NORTH.
or as a wind speed, i.e. | vH |, and direction. Particular care should be taken when dealing with the direction since two opposite conventions are commonly used:
- φVECT is the WIND VECTOR AZIMUTH, i.e. the direction TOWARDS which the wind is
blowing. It increases clockwise from North when viewed
from above. Terms such as northward, eastward etc. imply wind
vector azimuths.
- φMET is the METEOROLOGICAL WIND DIRECTION, i.e. the direction FROM which the wind is blowing. It also increases clockwise from North when viewed from above. Terms such as northerly, easterly etc. imply meteorological wind directions.
These directions are typically expressed in units of degrees, φ(deg), but can either be in the interval -180° to +180° or 0° to 360°. The wind vector azimuth and meteorological convention direction are related by:
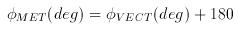
subtracting 360° where appropriate in order to keep the values within the desired range. Note that when writing a computer program to convert between speed/direction and orthogonal component conventions, the use of trigonometric functions assumes that angles are expressed in units of radians, φ(rad), rather than degrees (pocket calculators can typically perform trigonometric functions on angles expressed in either units). Directions are converted from units of degrees to radians through the relationship:
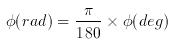
Moreover, the familiar expressions relating the x component of a vector to the cosine of its angle and the y component to its sine imply use of:
- φPOLAR which is the WIND VECTOR POLAR ANGLE in two-dimensions. It increases ANTICLOCKWISE FROM the +ve x-axis, i.e. from EAST; this in the opposite sense to the wind vector azimuth and the meteorological wind direction, and from a different origin.
When converting back from orthogonal components to speed and direction, the atan2(y,x) function should be used in order to avoid ambiguity in the returned value of the wind vector polar angle. The expressions below can be used to convert horizontal wind vector information directly between the orthogonal component and speed/direction conventions without the need for first converting directions between wind the vector polar angle and the wind vector azimuth or meteorological wind direction.
| Wind Vector Azimuth | Meteorological Wind Direction |
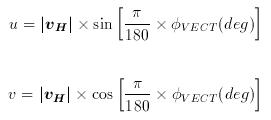
|
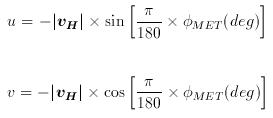
|
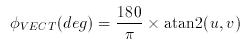
|
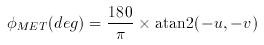
|
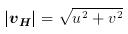
|
|

 THE NERC MST RADAR FACILITY AT ABERYSTWYTH
THE NERC MST RADAR FACILITY AT ABERYSTWYTH